
Matematika Blog
Selasa, 09 Juni 2020
Selamat Datang di Blog Matematika bersama Erna Pragusti purwati....
Definisi, Ciri & Contoh Segi Banyak Beraturan dan Tidak Beraturan
LIHATLAGI.COM, Penjelasan lengkap definisi, ciri-ciri serta contoh segi banyak beraturan dan tidak beraturan. Pada postingan ini juga terdapat bukan contoh segi banyak.
Pembelajaran tentang segi banyak beraturan dan tidak beraturan bisa ditemukan dalam pelajaran matematika pada buku tematik terpadu kelas 4 SD/MI tema 1 Indahnya Kebersamaan. Subtema 1 Keberagaman Budaya Bangsaku.
Apa itu segi banyak?
Daftar Isi
1. Definisi Segi Banyak
Segi banyak adalah bangun tertutup yang seluruh sisinya dibatasi oleh garis yang memiliki banyak segi dan sudut yang paling sedikit mempunyai tiga sisi.
Jadi pada bangun segi banyak ini garisnya tidak terputus, melainkan saling bersampung. Oleh sebab itulah disebut bangun tertutup.
Lihat contohnya di bawah ini.

Pada contoh di atas, angka-angka dengan warna merah menujukkan jumlah sudut. Sedangkan angka-angka warna biru menunjukkan jumlah sisi pada sebuah bangun datar segi banyak.
Gambar di atas juga membuktikan bahwa sudut segi banyak jumlahnya sama dengan jumlah sisi yang dimilikinya.
2. Ciri-ciri Segi Banyak
Barusan di atas sudah disinggung bahwa ciri segi banyak adalah memiliki jumlah sudut dan isi yang sama banyak. Perhatikan lagi gambar di atas.
Ciri-cirinya antara lain:
- Bangun tertutup
- Memiliki minimal 3 sudut
- Jumlah sudut sama banyak dengan jumlah sisi
- Sisinya dibatasi oleh garis lurus (tidak melengkung)
3. Contoh Segi Banyak
Yang termasuk ke dalam contoh segi banyak itu contohnya segi tiga, segi empat, segi lima, segi enam, bintang, jajar genjang, ketupat dan lain-lain.

Segi banyak terbagi 2, yaitu segi banyak beraturan dan tidak beraturan.
3.1. Contoh Beraturan
Segi banyak beraturan adalah bangun tertutup yang memiliki banyak sudut dan dibatasi oleh garis, dengan sisi sama panjang dan sudut sama besar.
Ciri-cirinya panjang sisi sama, besar sudut sama, dan bentuknya harus cembung.

Contoh yang beraturan:
- Segitiga sama sisi
- Bujur sangkar
- Pentagon
- Heksagon
- Heptagon
- Oktagon
- Nonagon
- Dekagon
3.2. Tidak beraturan
Sedangkan yang tidak beraturan adalah bangun yang sisi-sisi tidak sama panjang dan sudut-sudutnya tidak sama besar.
Ciri-cirinya antara lain panjang sisi tidak sama, sudut-sudut tidak sama, dan bentuknya bisa cembung dan cekung.

Contoh yang tidak beraturan:
- Segitiga sama kaki
- Segitiga siku-siku
- Persegi panjang
- Belah ketupat
- Jajaran genjang
- Trapesium
3.3. Bukan contoh segi banyak
Gambar di atas ini adalah contoh bukan segi banyak. Cirinya adalah sudutnya kurang dari tiga dan bangun tidak membentuk persegi.
Demikian, semoga bermanfaat.
Selamat Datang di Blog Matematika bersama Erna Pragusti Purwati....
Peluang: Pengertian, Materi, & Rumus Matematika
Pernahkah kalian bermain monopoli? Untuk dapat bermain monopoli, kalian harus melemparkan dadu, angka yang kemudian muncul merupakan jumlah jalan yang harus ditempuh oleh pelempar dadu.
Pelemparan dadu bermata 6 pada permainan monopoli ini akan menghasilkan angka 1, 2, 3, 4, 5, atau 6.
Kemungkinan keluarnya angka tertentu pada pelemparan dadu bermata 6 adalah satu contoh dari banyak contoh penerapan materi matematika peluang dalam kehidupan sehari-hari.
Contoh lain dari peluang pada kehidupan sehari hari adalah pelemparan uang koin.
Pada saat melemparkan koin, ada dua buah kemungkinan mengenai sisi yang muncul. Sisi yang pertama adalah sisi angka dan sisi yang kedua adalah sisi gambar.
Nah, kali ini materi yang akan kita bahas adalah mengenai peluang. Mari kita simak materi berikut ini,
Daftar Isi
Definisi Peluang Matematika
Peluang pada umumnya berarti kesempatan, namun pada matematika, peluang atau probabilitas adalah kemungkinan yang mungkin terjadi/muncul dari suatu peristiwa.
Terkadang kita mengukur sebuah peluang dengan angka, seperti “kemungkinannya sekitar 10%”, atau dengan perkataan, seperti, “ah itu tidak mungkin” atau “itu sudah pasti terjadi”.
Dalam angka, peluang selalu berkisar antara 0 sampai dengan 1. Dimana 0 menyatakan sebuah kejadian yang tidak mungkin terjadi dan 1 menyatakan sebuah kejadian yang pasti terjadi, dalam matematika hal ini dinotasikan sebagai
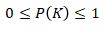
dengan P(K) menyatakan peluang terjadinya kejadian K.
Istilah yang Sering Digunakan
Di dalam materi peluang, ada beberapa istilah yang sering digunakan, diantaranya
Ruang sampel : Himpunan dari semua hasil percobaan yang mungkin terjadi
Titik sampel : Anggota dari ruang sampel
Kejadian : Himpunan bagian dari ruang sampel
Rumus Peluang
Sebelum membahas rumus peluang, terlebih dahulu kita akan membahas mengenai frekuensi relatif.
Frekuensi relatif adalah perbandingan dari banyak percobaan yang dilakukan dengan banyaknya kejadian yang diamati.
Frekuensi relatif dapat dicari dengan menggunakan rumus
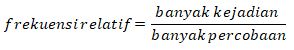
Apabila peluang dari setiap titik sampel dari anggota ruang sampel S sama, maka peluang kejadian K yang jumlah anggotanya ditulis sebagai n(K) dapat dicari dengan rumus
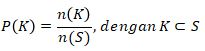
Contoh Soal
Pada pelemparan sebuah dadu, tentukan peluang munculnya sisi dadu yang berangka genap
Ruang sampel S adalah {1,2,3,4,5,6}
n(S) = 6
Sisi dadu genap adalah {2,4,6}
n(K) = 3
maka
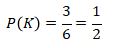
jadi, peluang munculnya mata dadu berangka genap adalah 0,5.
Kejadian Majemuk
Kejadian majemuk adalah kejadian baru yang terbentuk dari perlakuan pada dua atau lebih kejadian.
Kejadian Komplemen
Kejadian K komplemen adalah semua kejadian yang bukan kejadian K. Suatu kejadian K dan kejadian K komplemen (yang dinyatakan K’) memenuhi
P(K) + P(K’) = 1 atau P(K’) = 1 – P(K)
Contoh soal:
Ana bermain kartu bridge, kemudian diambil satu kartu secara acak. Tentukan peluang Ana mengambil kartu bukan As
jumlah semua kartu bridge
n (S) = 52
jumlah semua kartu As
n(K) = 4
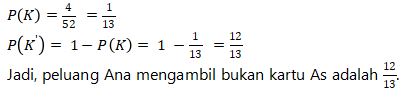
Penjumlahan Peluang
Kejadian saling lepas
Terdapat dua buah kejadian A dan B yang kemudian disebut kejadian saling lepas jika tidak ada elemen pada kejadian A yang sama dengan elemen yang terdapat pada kejadian B.
Peluang salah satu A atau B mungkin terjadi dengan A dan B adalah kejadian saling lepas, rumusnya adalah
P(A Ս B) = P(A) + P (B)
Contoh Soal
Terdapat dua buah dadu, biru dan hijau. Dua dadu tersebut kemudian dilempar secara bersamaan satu kali, tentukan peluang munculnya sisi dadu yang memiliki jumlah 3 atau 10!
Hasil pelemparan dadu tersebut kemudian dituliskan dalam tabel dibawah ini
| Dadu | Merah | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) | |
| Dadu | 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| Biru | 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) | |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) | |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
Munculnya mata dadu berjumlah 3
A = {(1,2), (2,1)}
n(A) = 2
Munculnya mata dadu berjumlah 10
B = {(4,6), (5,5), (6,4)}
Karena anggota A tidak ada yang sama dengan anggota B, maka kejadian A dan B merupakan dua kejadian yang saling lepas sehingga menggunakan rumus:

sehingga peluang munculnya mata dadu yang berjumlah 3 atau 10 adalah .
